[size=12pt] I was up late last night thinking about how Minecraft, from a design standpoint, is very hard to build “curvy” and “wavy” things in, for obvious reasons. The blocks are equivalent to an entire 1 meter by 1 meter pixel, and the stated “Blockiness” of said huge pixels make it hard to create things that are non-rectangular. It has been done before, but, to my knowledge, no one has ever attempted and/or documented building Non-Euclidean Objects in Minecraft (that can be tangible in the real world) and has documented it. With that, I bring you:
[size=24pt]Non-Euclidian Geometry in Minecraft
[size=18pt]Part 1: Releaux Triangles
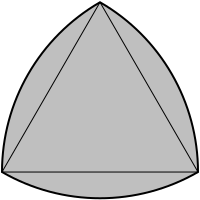
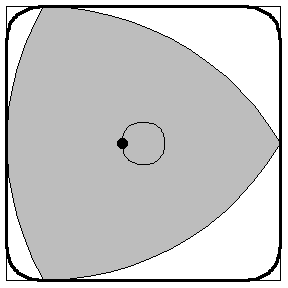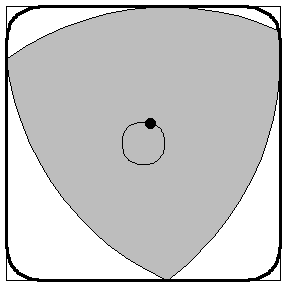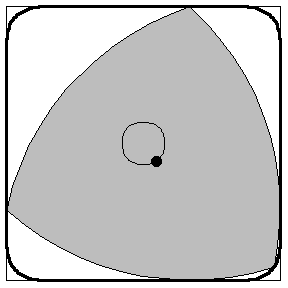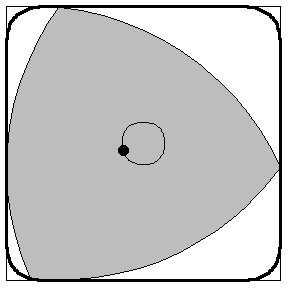
[size=12pt] First, let me define a Releaux [REL-A-OH] Triangle. A Releaux Triangle, as shown above, is a triangle that has rounded edges and all line segments passing through the center point of the triangle have the exact same width. As a result, this classifies as a “Shape of Constant Width.” This means that no matter how you turn it, it will have the same width from top to bottom.
For building in Minecraft, Releaux Triangles are quite difficult, as they are formed from the intersection of three circular disks, each having its center on the boundary of the other two. This picture below may better help you understand:

This method is the same method I employed to building my Releaux Triangles in Minecraft, Shown Below:
But Why Stop there? Why not make a 3D equivalent of this shape? To do this, we can create what's called a solid of revolution. Basically, we take this shape and we rotate it in a 3-dimensional space along it's vertical axis, leaving an image of the shape behind. Doing that, we get this acorn-esuqe shape:
These shapes could prove interesting to build buildings from, like having a Releaux triangle as the base of the building, while the Solid of Revolution version of the Triangle could provide and interesting house or building design in it of itself.
Well, it's getting late, and the inky blackness beckons my name. If there are any questions, comments, or concerns, feel free to leave your feedback. It is not only welcomed, but heavily encouraged.
Best Regards,
DC7